Mathematical modeling of physiological systems involves the use of mathematical equations to represent biological processes. These models allow us to simulate, analyze, and predict the behavior of complex physiological systems under various conditions. By creating mathematical abstractions of biological processes, researchers can gain insights into how the body functions, explore the effects of diseases, and optimize medical treatments.

Importance of Physiological Modeling

1. Prediction and Diagnosis:
   1. Models help predict the behavior of systems under different conditions, assisting healthcare professionals in diagnosing diseases and tailoring treatments. For example, in the case of respiratory diseases, a lung model can predict how ventilation will change with various treatment options.
2. Optimization and Personalization:
   1. Medical treatments, devices, and interventions can be optimized using models to simulate how they affect the patient. For example, ventilator settings can be adjusted based on lung mechanics simulations, ensuring a better fit for the patient’s needs.
3. Simulating Complex Systems:
   1. Some systems, like the human cardiovascular or respiratory systems, are too complex to study in their entirety through physical experiments. Mathematical models provide a way to simulate these systems and test different scenarios without putting patients at risk.

Commonly Used Models in Physiological Systems

Several different mathematical models are used across different physiological systems, including:

• Cardiovascular Models: Windkessel, lumped-parameter models, and more complex models of blood flow and pressure dynamics.
• Respiratory Models: Single Compartment Lung Model, multiple compartment models, and dynamic models for lung ventilation and gas exchange.
• Neurophysiological Models: Models for neural firing, brain activity, and network dynamics.
• Musculoskeletal Models: Models of muscle forces, joint movements, and mechanical interactions between bones and muscles.
• Pharmacokinetic Models: Drug absorption and distribution models for understanding the body’s interaction with medications.

Examples:

1. Single Compartment Lung Model

The Single Compartment Lung Model represents the lung as a single “lumped” compartment, simplifying the complexity of the lung’s structure. This model focuses on lung compliance (how the lung expands) and airway resistance (how the air flows through the airways). It is widely used in mechanical ventilation and for studying the effects of diseases on lung mechanics.

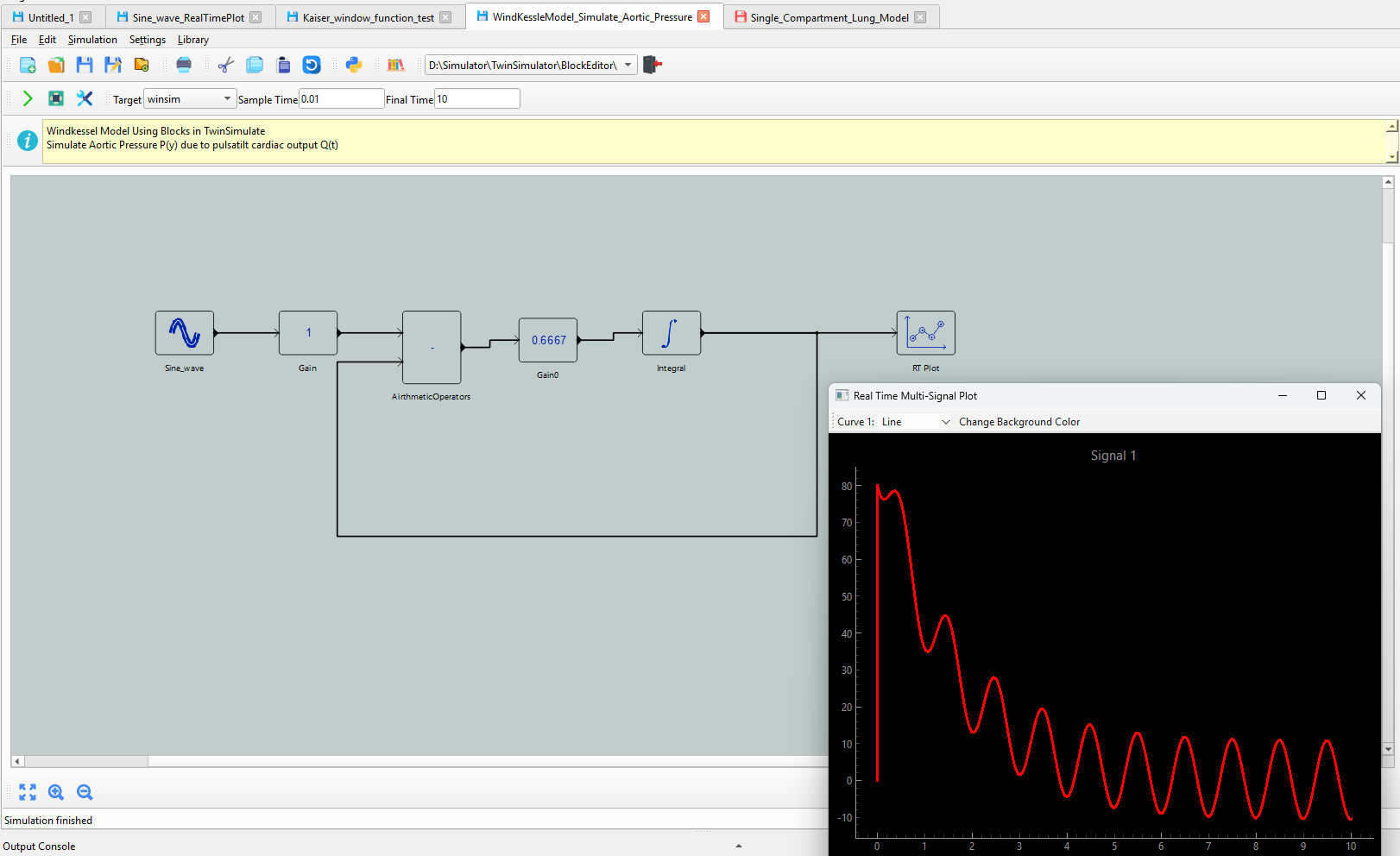
2. Windkessel Model

The Windkessel Model simplifies the arterial system by treating the arteries as a combination of a capacitor (representing compliance) and a resistor (representing vascular resistance). It is commonly used to study arterial pressure and blood flow dynamics. This model provides insight into how pressure waves propagate through the arteries and how various factors (e.g., age, disease) affect these dynamics.

Some example models available now in Twin Simulate

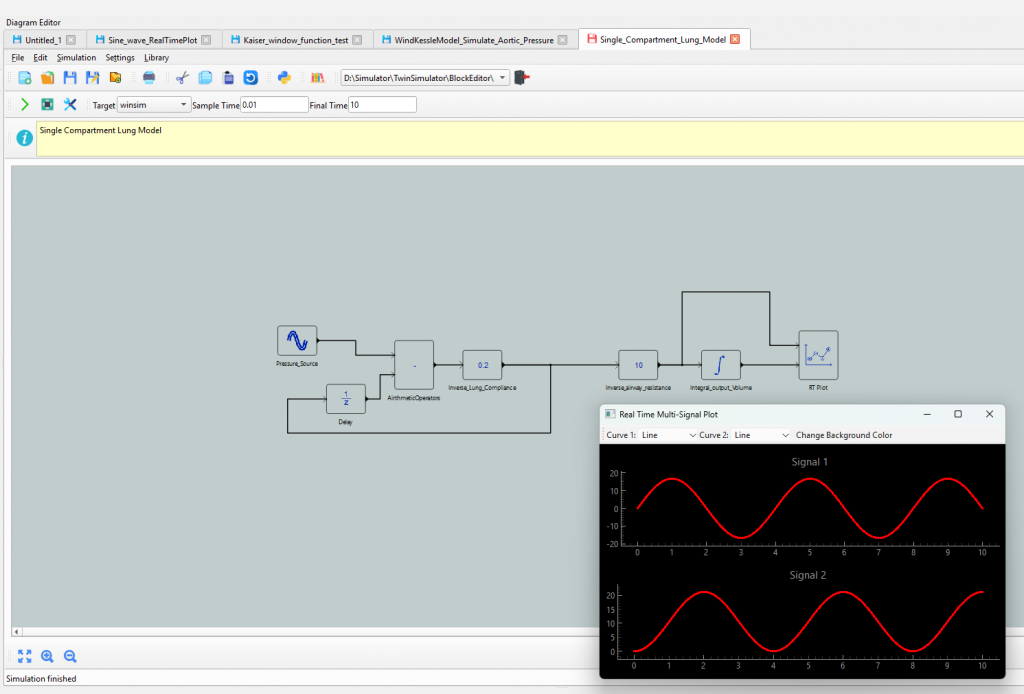
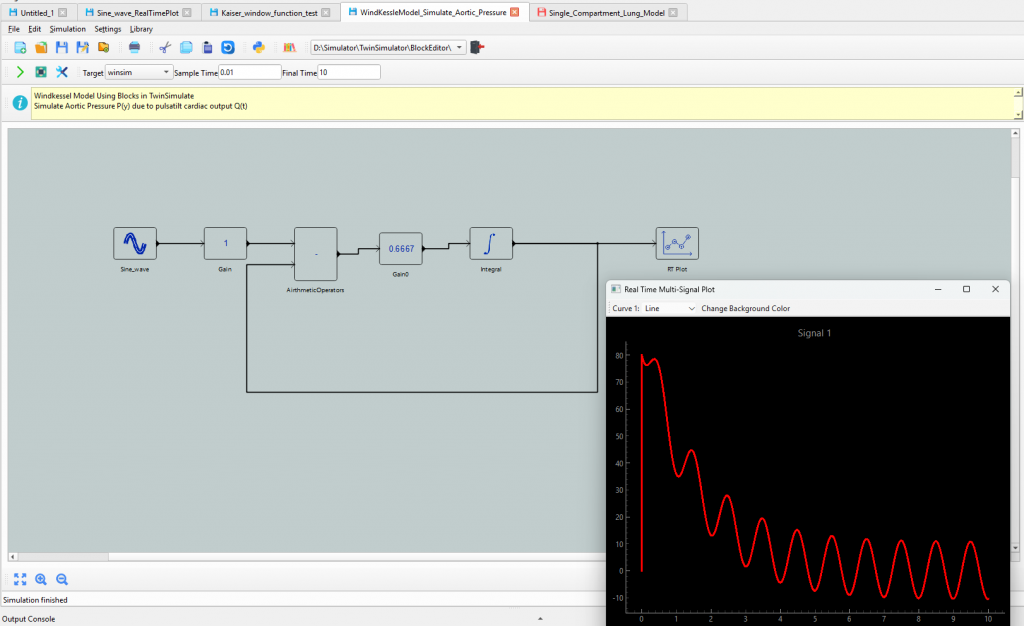
Reach out for obtaining a trial license and build and test your physiological models with Twin Simulate.